
Why do things crack? In a word: vibrations. Vibrations plus fatigue equal failure, where cyclic fatigue loading flexes parts or equipment back and forth until they crack. A major breakthrough in vibration theory is presented here, along with an vibration introduction and examples of pump damages.
Lord Rayleigh described vibrations in his “Theory of Sound”, which was published in the late 1800’s, but resonance has only recently been fully described. To do so, Newton’s differential equations of motion were solved by this author to establish new theory in a 2017 Pressure Vessel and Piping Conference paper (Shock Waves, Vibrations, and Resonance in Linearly Elastic Beams). In short, every structure or machine, and every component therein, vibrates at multiple frequencies, known as higher mode natural frequencies. These frequencies can now be graphically visualized. In particular, when motor speeds for a machine nearly equal any natural frequency, the vibrations are multiplied at that frequency to cause equipment damages.
Vibration Theory
The simplest example of vibration is a spring with a weight attached to it, where the spring has some damping. This spring-mass-damper system defines a single degree of freedom system, where this single vibration provides a simple description for real systems. A vibrating spring has a period that equals the time required to complete one vibration cycle; a frequency that equals the inverse of the period; an amplitude, or magnitude, of vibration; and a damping coefficient that controls the decrease in vibration magnitude to reach a constant equilibrium, or static, value that may or may not equal zero.

Vibration Model Of A Weight Dropped From A Spring At Rest
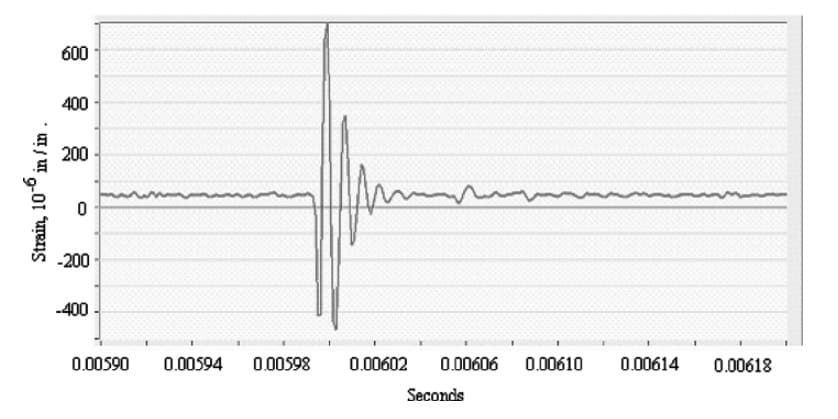
To better understand vibrations, consider the case of a constant force suddenly applied to a spring, i.e., a weight dropped from a spring at rest. To summarize this vibration performance, the dynamic load factor, or DLF, equals the maximum vibration amplitude (or stress) divided by the vibration amplitude (or stress) at the equilibrium or static condition. The DLF is reduced by damping, where common damping values in structures typically range between 1% and 2%, but may be as high as 10% or more. For suddenly applied loads in the absence of damping, the maximum DLF equals 2. The DLF may be further reduced due to the rate of loading or duration of loading. This application of DLF’s yields reasonable vibration approximations, when a load is applied perpendicular to a component surface. However, if that same load travels inside apipe, the DLF equals four (Leishear, 2013, Fluid Mechanics, Water Hammer, Dynamic Stresses, and Piping Design, ASME Press text book). The theory of DLF’s explained hundreds of thousands of piping failures (Water Main Failures – A Billion Dollar a year problem, Empowering Pumps). This very brief vibration introduction leads into a discussion of resonance.
Resonance Theory
When motor vibrations are applied to a pump, the pump reacts much differently than when subjected to a constant load. If the motor speed equals a natural frequency of that component, vibrations will significantly increase beyond expectations. In fact, vibrations would increase to infinity in the absence of damping, where damping reduces resonance effects to agree with observations. In short, maximum resonance occurs when the motor speed equals any one of the natural frequencies of components, where this phenomenon has finally been described after hundreds of years of vibration theory advances.
As examples, 1) structural vibrations of attached piping and equipment supports may vibrate at any one of their natural frequencies to crack that piping. 2) Vibration is a common failure cause for mechanical seals in pumps. 3) Damaged components like ball bearings vibrate at their natural frequencies, such that races, cages, and balls of that bearing each vibrate at their own frequencies – a very complex process.
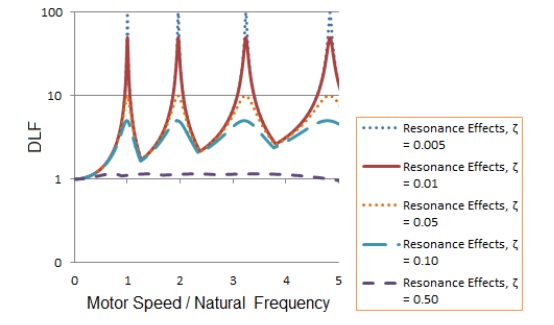

Vibration and Resonance Acceptance Criteria
For rotating equipment, a simple approach to assess vibration damage was presented in a 1950’s ASME Magazine article, and this approach is still used by many today. Measured vibrations are compared to acceptance limits for installed rotating equipment, such as fans, pumps, or compressors. Troubleshooting vibration problems requires that the vibration of the defective component be determined and corrected. Troubleshooting may sound simple, but a thorough knowledge of equipment construction, vibration principles, and equipment operations is essential to solve vibration failure problems. Prediction of specific rotating equipment vibration problems in advance is problematic, at best.
A Pump Motor Failure Example
For example, consider the failure of a ball bearing assembly in a 150 horsepower motor that operated a connected pump. The motor was reported to be noisier than usual, and could be heard at a distance of fifty feet from the motor. The ball bearings in the motor are constructed of inner and outer races that the balls roll between, and cages that separate the balls. The balls, cages, and races each have a specific frequency, and the ball spin frequency was displayed in the frequency spectrum since they were damaged. One of the bearings, the thrust bearing, was completely destroyed, and one of the races and several cages were broken. The other bearing vibrated at its ball spin frequencies, and the bearing that had not been destroyed. The vibrations were above 0.1 inch per second, and the bearings were in fact damaged. At the thrust bearing, the vibrations at the destroyed bearing location were lower than 0.1 inches per second. Since the thrust bearing was no longer in contact with the shaft, there were no associated vibrations. That is, the measured vibrations were not caused by the destroyed bearing assembly at all, but were measured from the bearing assembly that remained in service and was experiencing bearing vibration damages of its own. What about the noise levels? The vibrations of the bearing were inadequate to cause the low frequency rumbling sounds that were heard, where the vibration occurred at the frequencies of the grating on the steel mounting platform. In other words, the bearing vibration caused the platform to rattle the gratings enough to be heard fifty feet away. This resonance issue was far from obvious at the onset of troubleshooting, as with many complex vibration failures. The invention of new theory that is discussed here provides practicing engineers a new tool to better understand vibration failures.
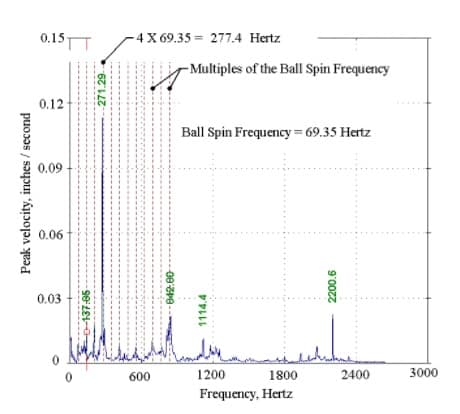
Frequencies of Vibration for a Damaged Ball Bearing Assembly
ROBERT A. LEISHEAR, an ASME Fellow, is a consulting engineer for Leishear Engineering, LLC, and he has a Ph. D in Mechanical Engineering and a nearly completed Ph.D. in Nuclear Engineering. Dr. Leishear has published nearly 70 publications on water hammer, vibrations, fluid mechanics, pumps, and explosions.



